A Voyage through Algorithms using Javascript - Selection Sort

What is Selection Sort?

Selection Sort is one of the elementary sorting algorithms in computer science. It divides the input list into two parts: a sorted portion at the left end and an unsorted portion at the right end. The algorithm repeatedly selects the smallest (or largest) element from the unsorted portion and moves it to the sorted portion.

How Selection Sort Works

Selection Sort works by iterating through the array, finding the minimum element in the unsorted portion, and swapping it with the first element of the unsorted portion. This process is repeated until the entire array is sorted.

Here’s a step-by-step breakdown:

1. Start with the first element as the “current” element.
2. Search through the rest of the array to find the smallest element.
3. If a smaller element is found, swap it with the “current” element.
4. Move to the next element and repeat steps 2-3 until you reach the end of the array.
5. The array is sorted when you’ve gone through all elements.

Visualization of Selection Sort:

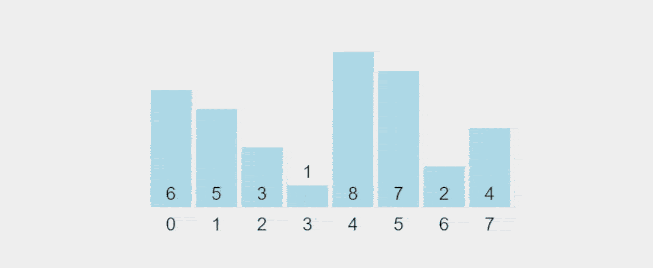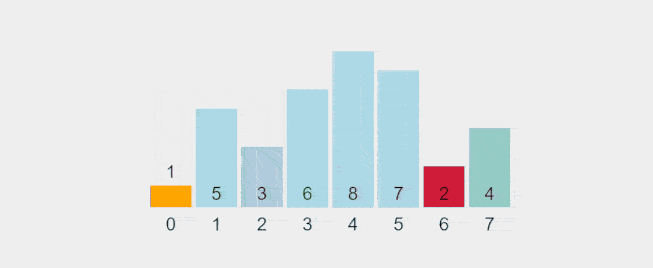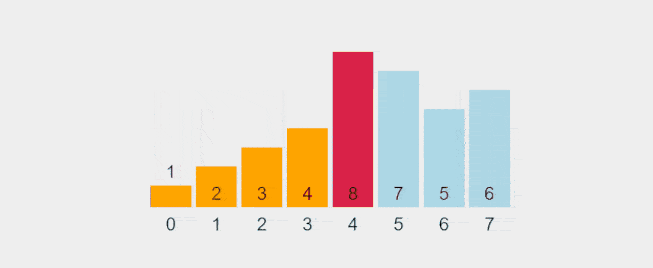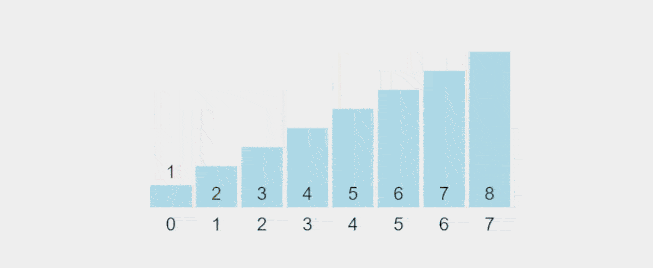
Recorded gif from https://visualgo.net/en/sorting

Implementing Selection Sort in JavaScript

Let’s take a look at the implementation of Selection Sort in JavaScript, with detailed comments explaining each part:

function selectionSort(arr) {
  // Cache the array length to avoid recalculating it in every loop iteration
  // This is a small optimization that can be beneficial for larger arrays
  const arrayLength = arr.length;
  let indexOfMinimum;

  // Outer loop: iterates through the array, establishing the boundary between sorted and unsorted portions
  // We only need to go up to the second-to-last element because the last element will already be in place
  for (let currentIndex = 0; currentIndex < arrayLength - 1; currentIndex++) {
    // Assume the current index holds the minimum value
    indexOfMinimum = currentIndex;

    // Inner loop: searches for the minimum element in the unsorted portion of the array
    // Start from the element next to currentIndex, as elements before currentIndex are already sorted
    for (let searchIndex = currentIndex + 1; searchIndex < arrayLength; searchIndex++) {
      // If we find a smaller element, update indexOfMinimum
      if (arr[searchIndex] < arr[indexOfMinimum]) {
        indexOfMinimum = searchIndex;
      }
    }

    // After inner loop, indexOfMinimum holds the index of the smallest element in the unsorted portion
    
    // Swap the found minimum element with the first element of the unsorted portion
    // Only swap if we found a smaller element (indexOfMinimum changed)
    if (indexOfMinimum !== currentIndex) {
      // Use destructuring assignment for a clean swap operation
      // This is a shorthand way to swap two array elements without a temporary variable
      [arr[currentIndex], arr[indexOfMinimum]] = [arr[indexOfMinimum], arr[currentIndex]];
    }
  }

  // The array is now sorted in-place
  return arr;
}

Key Points:

1. Outer Loop and Passes: The outer loop for (let currentIndex = 0; currentIndex < arrayLength - 1; currentIndex++) manages the “passes” through the array. Each iteration of this loop represents one complete pass, where we find the smallest element in the unsorted portion and place it in its correct position.
2. Inner Loop: Within each pass, the inner loop for (let searchIndex = currentIndex + 1; searchIndex < arrayLength; searchIndex++) searches for the minimum element in the unsorted portion of the array.
3. Swap After Inner Loop: Importantly, the swap operation occurs after the inner loop completes. This means we only perform one swap per pass, moving the found minimum element to its correct position.
4. Pass Completion: A pass is considered complete when the inner loop finishes and the swap (if necessary) is performed. The algorithm then moves to the next pass by incrementing currentIndex in the outer loop.
5. Optimization: We only swap if a new minimum is found (if (indexOfMinimum !== currentIndex)), avoiding unnecessary operations.

Most important point to understand Selection Sort is figuring out how it manages its passes:

• Each pass (outer loop iteration) finds the smallest element in the unsorted portion.
• The inner loop handles the comparison part of each pass.
• The swap after the inner loop finalizes each pass by placing the found minimum in its correct position.
• The process repeats, with the sorted portion growing by one element after each pass.

In other words, we don’t need to manually track when each pass ends - the nested loop structure naturally handles this for us.

Making Selection Sort Stable

While our basic implementation of Selection Sort works well, it has one potential drawback: it’s not stable. But what does this mean, and why might it matter?

Understanding Stability in Sorting

A stable sorting algorithm preserves the relative order of equal elements. This becomes important when sorting complex data or when you need to maintain the original order of equivalent items.

For example, consider this array: [4A, 3, 2, 4B, 1] (where 4A and 4B represent different elements with the same value 4).

Our current Selection Sort might produce: [1, 2, 3, 4B, 4A]

Notice how 4B and 4A swapped positions. In some scenarios, this could be problematic.

Implementing Stable Selection Sort

We can modify our algorithm to make it stable. Instead of swapping elements, we’ll shift elements and insert the minimum value in its correct position. Here’s how:

function stableSelectionSort(arr) {
  // Cache the array length to avoid recalculating it in every loop iteration
  const arrayLength = arr.length;
  
  // Outer loop: iterates through the array, establishing the boundary between sorted and unsorted portions
  // We only need to go up to the second-to-last element because the last element will already be in place
  for (let currentIndex = 0; currentIndex < arrayLength - 1; currentIndex++) {
    // Assume the current index holds the minimum value
    let indexOfMinimum = currentIndex;
    
    // Inner loop: searches for the minimum element in the unsorted portion of the array
    // Start from the element next to currentIndex, as elements before currentIndex are already sorted
    for (let searchIndex = currentIndex + 1; searchIndex < arrayLength; searchIndex++) {
      // If we find a smaller element, update indexOfMinimum
      if (arr[searchIndex] < arr[indexOfMinimum]) {
        indexOfMinimum = searchIndex;
      }
    }
    
    // After inner loop, indexOfMinimum holds the index of the smallest element in the unsorted portion
    
    // If the minimum element is not already in its correct position
    if (indexOfMinimum !== currentIndex) {
      // Store the minimum value
      const minimumValue = arr[indexOfMinimum];
      
      // Shift all elements between currentIndex and indexOfMinimum one position to the right
      // This maintains the relative order of equal elements, ensuring stability
      for (let shiftIndex = indexOfMinimum; shiftIndex > currentIndex; shiftIndex--) {
        arr[shiftIndex] = arr[shiftIndex - 1];
      }
      
      // Place the minimum value in its correct position
      arr[currentIndex] = minimumValue;
    }
  }
  
  // The array is now sorted in-place and in a stable manner
  return arr;
}

Key Points for Stable Selection Sort:

1. Outer Loop and Passes: Similar to the classic version, the outer loop for (let currentIndex = 0; currentIndex < arrayLength - 1; currentIndex++) manages the passes through the array. Each pass finds the smallest element in the unsorted portion and places it in its correct position.
2. Inner Loop: The inner loop for (let searchIndex = currentIndex + 1; searchIndex < arrayLength; searchIndex++) searches for the minimum element in the unsorted portion of the array, just like in the classic version.
3. Shifting Instead of Swapping: The key difference from the classic version is that after finding the minimum element, we don’t swap it directly. Instead, we shift all elements between the current position and the minimum element’s position one step to the right. This preserves the relative order of equal elements.
4. Insertion After Shifting: After shifting, we insert the minimum element into its correct position. This approach ensures stability by maintaining the original order of equal elements.
5. Additional Loop for Shifting: The stable version introduces an additional loop for the shifting operation: for (let shiftIndex = indexOfMinimum; shiftIndex > currentIndex; shiftIndex--). This loop moves elements to create space for the minimum element.
6. Preserving Stability: By shifting elements instead of swapping, we ensure that elements with equal values maintain their relative positions, making the sort stable.
7. Trade-off: The stable version potentially performs more write operations due to the shifting process, which can impact performance for larger datasets.

Most important point to understand Stable Selection Sort:

• The algorithm still selects the minimum element in each pass, but instead of swapping, it performs a series of shifts to insert the minimum element in its correct position.
• This shifting process is what guarantees stability, ensuring that equal elements maintain their relative order from the input array.
• The trade-off for stability is potentially more write operations, which can affect performance on larger datasets compared to the classic version.

In essence, stable selection sort maintains the overall structure of classic selection sort but modifies the element placement strategy to ensure stability at the cost of some additional operations.

Time and Space Complexity Analysis

Selection Sort’s performance characteristics are as follows:

• Time Complexity:

  • Best Case: O(n^2)
  • Average Case: O(n^2)
  • Worst Case: O(n^2)
• Space Complexity: O(1) - Selection Sort is an in-place sorting algorithm, requiring only a constant amount of additional memory.

Unlike Bubble Sort, Selection Sort’s time complexity remains quadratic even in the best case scenario. This is because it always scans the entire unsorted portion of the array to find the minimum element, regardless of whether the array is already sorted or not.

Advantages and Disadvantages of Selection Sort

Advantages:

• Simple to understand and implement
• In-place sorting (O(1) space)
• Performs well on small lists
• Minimizes the number of swaps (at most n swaps where n is the number of elements)

Disadvantages:

• Inefficient for large datasets (O(n^2))
• Not adaptive (doesn’t take advantage of existing order in the array)
• Not stable in its basic form (may change the relative order of equal elements)

When to Use Selection Sort

• Educational purposes: Its simplicity makes it excellent for teaching basic algorithm concepts.
• Small datasets: For very small arrays, the performance difference compared to complex algorithms may be negligible.
• Memory-constrained environments: Its in-place nature can be advantageous in extremely memory-constrained scenarios.
• When minimizing writes is important: Selection Sort performs the minimum number of swaps possible (at most n).

Practical Applications and Use Cases

While Selection Sort, like Bubble Sort, isn’t typically used in production environments for large-scale applications, it can still find use in certain scenarios:

1. Educational tools: It’s often used to introduce sorting algorithms and algorithm analysis in computer science education.
2. Embedded systems: In systems with very limited memory, its in-place sorting can be advantageous.
3. Small datasets: For sorting small lists (e.g., less than 50 elements), its simplicity might outweigh the performance benefits of more complex algorithms.
4. Minimizing writes: In scenarios where writing to memory is significantly more expensive than reading, Selection Sort’s minimal number of swaps can be beneficial.

Conclusion

Selection Sort, despite its inefficiencies with large datasets, offers valuable insights into the world of sorting algorithms and algorithm analysis. Its straightforward approach makes it an excellent teaching tool for beginners in computer science.

Key takeaways are:

• It’s simple to understand and implement.
• It has a consistent time complexity of O(n^2), making it inefficient for large datasets.
• It’s an in-place sorting algorithm, but not stable in its basic form (may change the relative order of equal elements).
• It performs well when minimizing the number of swaps is important.
• It’s primarily used for educational purposes and in scenarios with very small datasets or limited memory.

While you’re unlikely to use Selection Sort in production code for large-scale applications, understanding its mechanics and trade-offs is helpful for developing a comprehensive grasp of sorting algorithms. As we continue our voyage through algorithms, we’ll encounter more sophisticated sorting methods that build upon these fundamental concepts.

The best algorithm for a given task depends on the specific requirements, constraints, and characteristics of your data. Even though Selection Sort is not a typical algorithm you’d use for most cases, it still has its place as a stepping stone to give you a better perspective for more advanced concepts.